FOUNDATION FOR INTELLIGENT PHYSICAL AGENTS

FIPA CCL Content Language Specification

Document title	FIPA CCL Content Language Specification
Document number	XC00009A	Document source	FIPA TC C
Document status	Experimental	Date of this status	2000/08/22
Supersedes	None
Contact	fab@fipa.org
Change history
2000/08/22	Approved for Experimental

© 2000 Foundation for Intelligent Physical Agents - http://www.fipa.org/

Geneva, Switzerland

Notice

Use of the technologies described in this specification may infringe patents, copyrights or other intellectual property rights of FIPA Members and non-members. Nothing in this specification should be construed as granting permission to use any of the technologies described. Anyone planning to make use of technology covered by the intellectual property rights of others should first obtain permission from the holder(s) of the rights. FIPA strongly encourages anyone implementing any part of this specification to determine first whether part(s) sought to be implemented are covered by the intellectual property of others, and, if so, to obtain appropriate licenses or other permission from the holder(s) of such intellectual property prior to implementation. This specification is subject to change without notice. Neither FIPA nor any of its Members accept any responsibility whatsoever for damages or liability, direct or consequential, which may result from the use of this specification.

Foreword

The Foundation for Intelligent Physical Agents (FIPA) is an international organization that is dedicated to promoting the industry of intelligent agents by openly developing specifications supporting interoperability among agents and agent-based applications. This occurs through open collaboration among its member organizations, which are companies and universities that are active in the field of agents. FIPA makes the results of its activities available to all interested parties and intends to contribute its results to the appropriate formal standards bodies.

The members of FIPA are individually and collectively committed to open competition in the development of agent-based applications, services and equipment. Membership in FIPA is open to any corporation and individual firm, partnership, governmental body or international organization without restriction. In particular, members are not bound to implement or use specific agent-based standards, recommendations and FIPA specifications by virtue of their participation in FIPA.

The FIPA specifications are developed through direct involvement of the FIPA membership. The status of a specification can be either Preliminary, Experimental, Standard, Deprecated or Obsolete. More detail about the process of specification may be found in the FIPA Procedures for Technical Work. A complete overview of the FIPA specifications and their current status may be found in the FIPA List of Specifications. A list of terms and abbreviations used in the FIPA specifications may be found in the FIPA Glossary.

FIPA is a non-profit association registered in Geneva, Switzerland. As of January 2000, the 56 members of FIPA represented 17 countries worldwide. Further information about FIPA as an organization, membership information, FIPA specifications and upcoming meetings may be found at http://www.fipa.org/.

Contents

1 Scope. 1

1.1 Semantic Underpinnings. 1

1.2 Constraint Satisfaction Problem Definitions. 1

1.2.1 Standard Definition of Constraint Satisfaction Problems. 1

1.2.2 Expressing Choices and Choice Problems. 2

1.2.3 Constraint Satisfaction Problem Model Used in FIPA Constraint Choice Language. 2

1.3 Language Properties. 3

1.3.1 Search Termination and Complexity. 3

2 FIPA Constraint Choice Language Ontology. 4

2.1 Object Descriptions. 4

2.1.1 Choice Problem.. 4

2.1.2 Solution. 4

2.1.3 Solution List 5

2.1.4 Identifier 5

2.1.5 Range. 6

2.1.6 Value. 6

2.1.7 Value List 6

2.1.8 Variable. 7

2.1.9 Variable Assignments. 7

2.1.10 Variable Name. 7

2.1.11 Exclusion. 8

2.1.12 Relation. 8

2.1.13 Domain Range. 9

2.1.14 Domain Role Term.. 9

2.1.15 Domain Term.. 9

2.1.16 Domain Variable Type. 10

2.1.17 Symbol 10

2.1.18 Index Pair 10

2.2 Function Descriptions. 10

2.2.1 Give Constraints for Information Gathering. 11

2.2.2 Give Values for Information Gathering. 11

2.2.3 Solving to Generate Solutions. 13

2.2.4 Solving to Generate a List of Solutions. 13

2.3 Propositions. 14

2.3.1 Insoluble. 14

2.3.2 Soluble. 14

2.3.3 Unknown. 14

2.3.4 Is a Constraint Satisfaction Problem.. 14

2.3.5 Is an Action Result 15

2.4 Ontology Requirements. 15

3 References. 16

4 Normative Annex A — FIPA-CCL XML Based Concrete Syntax. 17

4.1 XML DTD. 17

5 Informative Annex B — Language Usage. 20

5.1 Step 1: Problem Modelling. 20

5.1.1 FIPA Constraint Choice Language Constraint Representations. 20

5.2 Step 2: Information Gathering. 22

5.2.1 Using Tags to Separate Information from Different Sources. 22

5.3 Step 3: Information Fusion. 22

5.3.1 Using Tags for Information Fusion. 22

5.3.2 Information Fusion for Constraint Satisfaction Problems with Non-identical Variable Sets. 24

5.4 Step 4: Problem Solving. 25

5.4.1 Simple Constraint Satisfaction Problem Search Algorithm.. 26

5.5 References. 26

1 Scope

This document gives the specification of the Constraint Choice Language (CCL) which is designed as a language to be used for agent communication, and more specifically as a content language to be used with FIPA ACL (see [FIPA00061]).

The language is primarily intended to enable agent communication for applications that involve exchanges about multiple interrelated choices. FIPA CCL is based on the representation of choice problems as Constraint Satisfaction Problems (CSPs) and supports:

· Problem representation,

· Information gathering,

· Information fusion, and,

· Access to problem solution techniques.

Further information and additional resources concerning the use of FIPA CCL are available at:

http://liawww.epfl.ch/CCL/

1.1 Semantic Underpinnings

As already indicated, the FIPA CCL language is based on the representation of choice problems as CSPs. The CSP formalisms can therefore be used as a framework for defining the properties of the language and as a support for defining its semantics.

1.2 Constraint Satisfaction Problem Definitions

1.2.1 Standard Definition of Constraint Satisfaction Problems

Constraint Satisfaction Problems have been an intensive area study for some 30 years now and the basic definition of a CSP has remained unchanged since the early 1970s (see [Waltz75] for example). A finite binary discrete CSP is defined by:

· A finite set of variables V,

· A finite domain D_i of possible discrete values for each variable v_i Î V, and,

· A finite set of constraints C between any pairs of variables in V.

A solution to the CSP is defined as:

An assignment of values to variables such that: each variable v_i Î V is assigned a value d Î D_i, and none of the constraints c Î C are violated.

A solution therefore consists of finding consistent legal to assignment of values to each variable such that all the constraints posted for the problem are respected. More formal definitions can be found in [Mackworth77] and [Dechter92] amongst others. The basic definition has previously been extended in many ways, for example:

· Allowing dynamic sets of variables,

· Allowing dynamic, continuous or infinite variable domains, and,

· Allowing constraints of up to arity N where N = |V|.

These extensions are in general well defined and each has its own body of literature discussing appropriate solution techniques and application areas.

1.2.2 Expressing Choices and Choice Problems

Having defined CSPs, a choice problem can be defined as a CSP in the following way:

· Variables are choices to be made, such as which brand of shampoo to use or how many roses to buy for a date. The set of variables V is the set of interrelated choices which all need to be made to have a complete solution to the current problem.

· Domains are the available options for each choice (variable). Thus the number of roses may be anywhere between 1 and 30 and the brands of shampoo one of X, Y and Z. The assignment of one of the values from a domain D_i to a variable v_i corresponds to making a choice for v_i. The set of all possible combinations of assignments of domain values to variables define the problem search space.

· Finally Constraints are relationships between choices which express valid or invalid combinations. The set of constraints C therefore restricts the set of all possible combinations of choices to a smaller set of desirable assignments which meet the requirements of a solution to the choice problem.

The aim of the FIPA CCL language is therefore to leverage this formulation of a choice problem for use in agent communication. CSP techniques have been successfully applied to domains as diverse as configuration, planning, scheduling, design, diagnosis, truth maintenance, spatial reasoning logic programming and resource allocation. Using such a flexible problem representation as the basis for FIPA CCL will hopefully make it useful for a wide range of agent applications. Section 5, Informative Annex B — Language Usage gives a more detailed guide to how FIPA CCL can be used to model, communicate about and solve choice problems.

1.2.3 Constraint Satisfaction Problem Model Used in FIPA Constraint Choice Language

The CSP model which underlies FIPA CCL has three restrictions imposed which have been made to make the model minimal and more suitable for a communication language:

1. Binary Constraints. All constraints expressed must have an arity of no more than 2 (i.e. constraints are only ever between two variables. This restriction is often made in the CSP field, since most powerful solving techniques only apply to CSPs with arity 2 constraints. Furthermore, for discrete CSPs, any CSP represented in a form using n-ary constraints can be transformed into an equivalent CSP using only binary (2-ary) constraints. The language therefore looses none of its expressive power with this restriction.

2. Discrete Variable Domains. CSPs with only discrete sets of values in each variable domain are by far the best understood in the literature. Solving CSPs with ranges of continuous real values for value domains requires specialised solving techniques, therefore they are excluded in this version of the language. In practice, CSPs requiring continuous values are often be formulated by discretizing the continuous domain (so that discrete CSP solving techniques can be applied, see [SamHaroud96]).

3. Intensional Relations. There are two main ways of representing constraints for CSPs – as extensional relations (consisting of a list of the valid combinations of values for a pair or tuple of variables) and as intensional relations (consisting of relations such as equals, greater-than etc. which do not rely on an explicit list). FIPA CCL excludes the use of extensional relations – this makes CSPs expressed in FIPA CCL much easier to compose (merge) when fusing information from several sources. Once again, no expressive power is lost since it can be shown that for discrete CSPs every formulation using extensional constraints has an equivalent formulation using only intensional constraints.

There are also several implicit constraints which arise out of the fact that that CSPs represented in FIPA CCL must be contained in a single message:

· The number of variables must be finite (since they must be encapsulated in a single message), and,

· The number of constraints must be finite (since they must be encapsulated in a single message).

1.3 Language Properties

Given the CSP representation in previous sections, the following sections make statements about the formal properties of FIPA CCL.

1.3.1 Search Termination and Complexity

The basic underlying representation used in FIPA CCL is that of a CSP. In a sense most messages in FIPA CCL will define a problem (a CSP) which acts as an, as yet, unexplored solution space. This allows us to make definitive statements about when these problems have solutions, when a search is guaranteed to terminate and how long the search might take.

Questions of termination depend upon the type of CSP represented and on the state of the variable domains as follows:

· If all variable domains are discrete (as they must be given the restrictions in Section 0) and finite, then the solution and search spaces are both finite and search is guaranteed to terminate.

· Although the search for a solution can be shown to terminate, solving the problem is in general NP-complete. This is to be expected since the choice problems agents using FIPA CCL are trying solve are by their very nature combinatorially explosive.

· It has been shown that for some restricted types of CSP problem the complexity of finding a solution may be less than NP-complete: linear or polynomial for example (for example, see [Freuder82] and [vanBeek97]).

An important advantage gained by using the underlying CSP representation is that problem solving can leverage the powerful techniques which have been developed for CSP solving (there is extensive literature on this subject and [Tsang94] provides a good starting point). Techniques exist which routinely solve problems of over 1000 variables and most problems of 10-20 variables can be solved using very simple search algorithms.

2 FIPA Constraint Choice Language Ontology

2.1 Object Descriptions

This section describes a set of frames, that represent the classes of objects in the domain of discourse within the framework of the FIPA-CCL ontology.

The following terms are used to describe the objects of the domain:

· Frame. This is the mandatory name of this entity, that must be used to represent each instance of this class.

· Ontology. This is the name of the ontology, whose domain of discourse includes the parameters described in the table.

· Parameter. This is the mandatory name of a parameter of this frame.

· Description. This is a natural language description of the semantics of each parameter.

· Presence. This indicates whether each parameter is mandatory or optional.

· Type. This is the type of the values of the parameter: Integer, Word, String, URL, Term, Set or Sequence.

· Reserved Values. This is a list of FIPA-defined constants that can assume values for this parameter.

2.1.1 Choice Problem

This object represents a choice problem. For a CSP object to be well defined, the items in the exclusion and relations parameters must only refer to variables which are present in the Variables parameters. If the csp-ref parameter is not empty, then the CSP referenced in this parameter is taken to be the object of the csp-identifier object and the items in the variables, relations and exclusions fields are ignored. A CSP object which contains no variables, relations or exclusions (directly or by reference) is known as a null CSP.

Frame Ontology	csp FIPA-CCL
Parameter	Description	Presence	Type	Reserved Values
csp-ref	This references a CSP object.	Mandatory	csp-identifier
variables	Represents the choices which need to be taken in the choice problem. The variables listed in this parameter must all have unique names. The Variables listed in this parameter should have unique Role/Type combinations.	Optional	Set of csp-variable
relations	Represent the relationships between the choices to be made.	Optional	Set of csp-variable
exclusions	Represents a list of unary relations on single variables which exclude certain values from variable domains	Optional	Set of csp-variable

2.1.2 Solution

This object captures the notion of a solution to a choice problem. Here all the choices are assigned an appropriate value (one of the options) and the assignment violates none of the posted constraints.

Frame Ontology	csp-solution FIPA-CCL
Parameter	Description	Presence	Type	Reserved Values
csp-ref	This references a CSP object that the solution is for.	Mandatory	csp-identifier
assignments	A list of variable assignments such that the list contains one and only one assignment for each and every variable defined in the CSP reference in the CSP-ref slot, and, the assignment of these values violates none of the constraints posted for the CSP in the csp-ref parameter. That is, the variable assignment must be consistent.	Mandatory	Set of csp-variable-assignment

2.1.3 Solution List

This object captures the notion of a list of solutions to a choice problem.

Frame Ontology	csp-solution-list FIPA-CCL
Parameter	Description	Presence	Type	Reserved Values
csp-ref	This references a CSP object that the list of solutions is for.	Mandatory	csp-identifier
solutions	This is a list of possible solutions to the choice problem. The list must contain at least one such solution and may contain any subset of the whole set of solutions for the CSP.	Mandatory	Set of csp-solution

2.1.4 Identifier

This object represents the unique identifier of a CSP.

Frame Ontology	csp-identifier FIPA-CCL
Parameter	Description	Presence	Type	Reserved Values
identifier-body	This is the unique identifier of the CSP.	Mandatory	Symbol

2.1.5 Range

This object represents a complete domain, to be used when explicit enumeration of values would be too inefficient. The two items range and tuple-range are optional however one or the other must be present.

Frame Ontology	csp-range FIPA-CCL
Parameter	Description	Presence	Type	Reserved Values
range	This defines complete domains such as ordered lists of number numbers, world-airports, etc., which must be part of a common ontology.	Optional	domain-range
tuple-range	This defines a combination of all the legal values in a tuple. A range is given for each slot in the tuple and this parameter specifies that all combinations of values from the given ranges in each slot in the tuple are legal.	Optional	Set of domain-range

2.1.6 Value

This object represents an option. In general this can be a tuple and hence, the variable is an ordered list of domain terms.

Frame Ontology	csp-value FIPA-CCL
Parameter	Description	Presence	Type	Reserved Values
npart	This identifies the number of elements of the tuple value which must be identical to the number of items in the elements parameter.	Mandatory	Number
elements	This gives a list of values: one for each of the elements in the tuple.	Mandatory	Set of domain-term
tags	This contains a list of symbols that allow selective constraints.	Optional	Set of Symbol

2.1.7 Value List

This object represents a list of options. Each option is a tuple and each of the values in the list must have the same number of elements in the tuple; the number of elements must in turn be equal to the value of the npart parameter.

Frame Ontology	csp-value-list FIPA-CCL
Parameter	Description	Presence	Type	Reserved Values
npart	This identifies the number of elements of the tuple value which must be identical to the number of items in the elements parameter.	Mandatory	Number
value-list	This gives a list of values: one for each of the elements in the tuple.	Mandatory	Set of (Set of domain-term)
tags	This contains a list of symbols that allow selective constraints.	Optional	Set of Symbol

2.1.8 Variable

This object represents a single choice to be made, along with a set of possible options for that choice. The type and role parameters enable this object to be situated within the problem solving context.

Frame Ontology	csp-variable FIPA-CCL
Parameter	Description	Presence	Type	Reserved Values
name	This gives a unique symbol that is used to make references to the variable within the context of a single CSP.	Mandatory	Symbol
type	This specifies the type of values that the variable takes which includes granularity. An ordered list is used since the variable might take tuple values. In this case, the first type refers to the type of the first element in the tuple, etc.	Mandatory	Set of domain-variable-type
role	This identifies the position of the variable within the problem-solving context.	Optional	Set of domain-role-term
domain	This lists the possible values this variable object may take, that is, the available options. These options must be consistent with the types of values given in the type parameter.	Optional	csp-range | Set of csp-value

2.1.9 Variable Assignments

This object represents the assignment of a variable with a value. The variable named in the name parameter is assigned the value given in the value parameter. This represents a variable instantiation, that is, a choice being made.

Frame Ontology	csp-variable-assignment FIPA-CCL
Parameter	Description	Presence	Type	Reserved Values
name	This is the name of the variable having a value assigned to it.	Mandatory	csp-variable-name
value	This is value being assigned which must match with the type of the variable.	Mandatory	csp-value

2.1.10 Variable Name

This object represents the name of a variable in a CSP.

Frame Ontology	csp-variable-name FIPA-CCL
Parameter	Description	Presence	Type	Reserved Values
name	This name of a variable (choice).	Mandatory	Symbol

2.1.11 Exclusion

This object represents a constraint on a single variable by specifying a set of values that is explicitly disallowed for this variable.

2.1.12 Relation

This object represents a relation between two variables. Any variables named in the Relation-body must appear in the set of Variables of the relation. The indices parameter identifies which slots in a tuple valued variable are covered by the relation. For example, for an equality relation between two variables with 3 tuples as values (for example, (x, y, z)), setting the set of indices to ((2,2), (3,3)) indicates that only the 2nd and 3rd slot of the value tuples need ever be equal – the constraint is not violated even if the values in the 1st slots are unequal.

Frame Ontology	csp-relation FIPA-CCL
Parameter	Description	Presence	Type	Reserved Values
variables	This contains two variable names such that the named variables are defined in the current CSP[1].	Mandatory	Set of csp-variable-name
relation-type	This is the type of the relation being applied.	Mandatory	String	Intentional-Equality Intentional-Inequality Intensional-GreaterThan Intensional-LessThan Intensional-GreaterThanEqual Intensional-LessThanEqual Intensional-Empty
indices	This specifies what sub-fields of variable values the relation refers to.	Mandatory	Set of index-pair
tags	This contains a list of symbols that allow selective constraints.	Optional	Set of Symbol

Table 1 describes the allowed relations which can be specified in relation-type.

Relation Type	Description
Intentional-Equality	This specifies that all the variables listed in the variables parameter of the relevant CSP object and must take equal values in any instantiation.
Intentional-Inequality	This specifies that all the variables listed in the variables parameter of the relevant CSP object and must take strictly different values in any instantiation.
Intensional-GreaterThan	This specifies that the variables in the variables list of the relevant CSP object are related by a “greater than” relationship such that the order of the tuple defines the order in the relationship; the first variable in the list is strictly greater than the second, which is strictly greater than the third, etc. Note that this relation is only valid for variable types which have an ordering relation defined in the domain ontology (integers, for example).
Intensional-LessThan	This specifies that the variables in the variables list of the relevant CSP object are related by a “less than” relationship such that the order of the tuple defines the order in the relationship; the first variable in the list is strictly less than the second, which is strictly less than the third, etc. Note that this relation is only valid for variable types which have an ordering relation defined in the domain ontology (integers, for example).
Intensional-GreaterThanEqual	Similar to the Intensional-GreaterThan relation but using a “greater than or equals” relation.
Intensional-LessThanEqual	Similar to the Intensional-GreaterThan relation but using a “less than or equals” relation.
Intensional-Empty	This specifies that there are no allowed combinations of values for these values.

Table 1: Variable Relationship Types

2.1.13 Domain Range

Frame Ontology	domain-range FIPA-CCL
Parameter	Description	Presence	Type	Reserved Values
domain-range-body	This is a symbol defined in this ontology.	Mandatory	String

2.1.14 Domain Role Term

Frame Ontology	domain-role-term FIPA-CCL
Parameter	Description	Presence	Type	Reserved Values
domain-role-term-body	This is a symbol defined in this ontology.	Mandatory	String

2.1.15 Domain Term

Frame Ontology	domain-term FIPA-CCL
Parameter	Description	Presence	Type	Reserved Values
domain-term-body	This is a symbol defined in this ontology.	Mandatory	String

2.1.16 Domain Variable Type

Frame Ontology	domain-variable-type FIPA-CCL
Parameter	Description	Presence	Type	Reserved Values
domain-variable-type-body	This is a symbol defined in this ontology.	Mandatory	String

2.1.17 Symbol

This object is used to identify particular instances of objects. Symbols should be unique in their context of use.

Frame Ontology	Symbol FIPA-CCL
Parameter	Description	Presence	Type	Reserved Values
symbol-body	This is a unique word that is used to identify a particular instance of an object.	Mandatory	String

2.1.18 Index Pair

This object is used in relations to reference the individual fields in tuples. Given two variables with tuple valued variables, the this object indicates a field in the first and a field in the second which are somehow related.

Frame Ontology	index FIPA-CCL
Parameter	Description	Presence	Type	Reserved Values
index-body	This is a pair of numeric values which are used to identify which two particular fields in a tuple are related	Mandatory	Set of Integer

2.2 Function Descriptions

The following tables define usage and semantics of the functions that are part of the FIPA-CCL ontology.

The following terms are used to describe the functions of the FIPA-CCL domain:

· Function. This is the symbol that identifies the function in the ontology.

· Ontology. This is the name of the ontology, whose domain of discourse includes the function described in the table.

· Description. This is a natural language description of the semantics of the function.

· Domain. This indicates the domain over which the function is defined. The arguments passed to the function must belong to the set identified by the domain.

· Range. This indicates the range to which the function maps the symbols of the domain. The result of the function is a symbol belonging to the set identified by the range.

· Arity. This indicates the number of arguments that a function takes. If a function can take an arbitrary number of arguments, then its arity is undefined.

2.2.1 Give Constraints for Information Gathering

This action is used to collect constraints on a given set of variables and domains (that is, those specified in the CSP_T). The information is captured in a new CSP – CSP_INF which is a copy of CSP_T containing new constraints (and potentially new variables which are required for expressing these new constraints). The two CSPs (CSP_T and CSP_INF) could now be composed using one of the two main composition operations (conjunctive or disjunctive composition – see Section 5.3.2, Information Fusion for Constraint Satisfaction Problems with Non-identical Variable Sets). However it should be noted that this composition is not part of the csp-give-constraints action.

· Using csp-give-constraints followed by a conjunctive composition of CSP_T and CSP_INF creates a CSP whose solutions satisfy both the actor’s constraints and the constraints originally present in CSP_T.

· Using csp-give-constraints followed by a disjunctive composition of CSP_T and CSP_INF creates a CSP whose solutions satisfy either the original constraints in CSP_T or the constraints of the actor or both.

An agent can perform the csp-give-constraints iff it knows all variables v_i and all constraints c_i identifying the problem P to solve (either by understanding the CSP sent in the message or having access to the CSP referred to in the csp-ref reference).

Function	csp-give-constraints
Ontology	FIPA-CCL
Description	The expected effect of this function is the creation of a new CSP (CSPINF) containing information the agent carrying out the action (the actor) wishes to express about the choice problem defined by the CSP given in target of the action (CSPT). CSPINF consists of: · A complete copy of CSPT , including: all the variables originally present in CSPT (with their original roles and types), all the values in the variable domains of these variables and all the constraints present in CSPT. · New information in the form of constraints between variables vi specified in CSPT, i.e.: - Relations between variables vi, - Exclusions on variable domains of vi. · CSPINF may also include new variables (with associated domain values) which are added as part of the expression of constraints (when expressing ternary constraints in their binary representation for example – see Section 5, Informative Annex B — Language Usage).
Domain	csp / csp-identifier
Range	If the action could be successfully performed, then a CSP object representing the new CSPINF is generated. All new elements (those not present in CSPT ), including constraints, domain values and variables in CSPINF must include a tag in their tags field. This tag should be: the same for each element (this identifies all added information as being the result of a single information gathering action) and not present as a tag in the CSPT (ensuring that the information does not become mixed with existing information). If the csp-give-constraints function contains a csp-identifier referring to a CSP which the receiving agent has no knowledge of, then csp-unknown proposition is the result of the function.
Arity	1

2.2.2 Give Values for Information Gathering

This function is used to collect suitable options for a certain problem solving context. The CSP given as argument specifies a list of variables whose types, roles and relations identify the requested values. The two CSPs (CSP_T and CSP_INF) could now be composed using one of the two main composition operations (conjunctive or disjunctive composition – see Section 5.3.2, Information Fusion for Constraint Satisfaction Problems with Non-identical Variable Sets). However it should be noted that this composition is not part of the csp-give-constraints function.

· Using csp-give-values followed by a conjunctive composition of CSP_T and CSP_INF creates a CSP whose solutions only contain value assignments which are acceptable to both the actor and the agent(s) creating the original CSP_T.

· Using csp-give-values followed by a disjunctive composition of CSP_T and CSP_INF creates a CSP which includes an extended set of options (and possibly solutions) beyond those available in the original CSP_T .

An agent can perform the csp-give-values iff it knows all variables v_i and all constraints c_i identifying the problem P to solve.

Function	csp-give-values
Ontology	FIPA-CCL
Description	The expected effect of this function is the creation of a new CSP (CSPINF) containing information the agent carrying out the function (the actor) wishes to express about the choice problem defined by the CSP given in target of the function (CSPT). CSPINF consists of: · A copy of all the variables vi in CSPT including their original roles and types but not including the values in their domains, · New information in the form of values added to the domains of variables vi in CSPINF : - A new value is added to the domain of variable v iff the actor considers this value suitable as an assignment for variable v in a solution to the choice problem defined by CSPT. Values may be taken from the original domains of the variables in CSPT or be obtained from other sources. - If the actor knows of no suitable values for the domain of a particular variable then the domain is left empty. · CSPINF may also include new constraints (exclusions and relations) between the variables since these new constraints apply to the values being given as information by the execution of the function. New variables may be added as part of the expression of these constraints (when expressing ternary constraints for example).
Domain	csp / csp-identifier
Range	If the function could be successfully performed, then a CSP object representing the new CSPINF is generated. All new elements (those not present in CSPT ), including constraints, domain values and variables in CSPINF must include a tag in their tags field. This tag should be: the same for each element (this identifies all added information as being the result of a single information gathering function) and not present as a tag in the CSPT (ensuring that the information does not become mixed with existing information). If the csp-give-values function contains a csp-identifier referring to a CSP which the receiving agent has no knowledge of, then csp-unknown proposition is the result of the function.
Arity	1

2.2.3 Solving to Generate Solutions

This is the function of solving a CSP (the CSP specified as the subject parameter of the function). In order to perform this function an agent must be able to understand the CSP problem representation, that is, all of the variables and constraints.

Function	csp-solve
Ontology	FIPA-CCL
Description	The expected effect of having performed this function is to find an assignment of values to the variables vi in the CSP specified as the target of the function CSPT such that none of the constraints ci specified in CSPT are violated.
Domain	csp / csp-identifier
Range	If a solution to the problem identified by the csp-solve function (CSPT) exists then it is represented by a resulting csp-solution object. If there exist no solutions to the CSP identified of the csp-solve function, then a csp-insoluble proposition is the result of the function. If the csp-solve function contains a csp-identifier referring to a CSP which the receiving agent has no knowledge of, then a csp-unknown proposition is the result of the function.
Arity	1

2.2.4 Solving to Generate a List of Solutions

This function is similar to the csp-solve function but is defined as solving the CSP given in the subject parameter to return all of its solutions and collating these into a list of solutions.

Function	csp-solve-list
Ontology	FIPA-CCL
Description	The expected effect of having performed this function is to find one or several sets of assignments of values to the variables vi in the CSP specified as the target of the function CSPT such that none of the constraints ci specified in CSPT are violated.
Domain	csp / csp-identifier
Range	If a solution or set of solutions to the problem identified by the csp-solve function (CSPT) exists then it is represented by a resulting csp-solution-list object. If there exist no solutions to the CSP identified in the csp-solve-list function, then a csp-insoluble proposition is the result of the function. If the csp-solve-list function contains a csp-identifier referring to a CSP which the receiving agent has no knowledge of, then a csp-unknown proposition is the result of the function.
Arity	1

2.3 Propositions

A proposition makes a statement about the truth or falsity of a property of a CSP object. Note that the definitions given in this section are effectively proposition schemas expressed as predicates. However, once the variables in the schemas are instantiated the ensemble is treated as a proposition.

2.3.1 Insoluble

This states that the CSP given in the subject parameter has no solutions.

Proposition	csp-insoluble
Ontology	FIPA-CCL
Description	This proposition is true iff ^Ø$ X such that X is an assignment of values to the variables of the given CSP consistent with the given constraints.
Domain	csp / csp-identifier

2.3.2 Soluble

This states that the CSP given in the subject parameter has at least one solution.

Proposition	csp-soluble
Ontology	FIPA-CCL
Description	This proposition is true iff $ at least an X such that X is an assignment of values to the variables of the given CSP consistent with the given constraints.
Domain	csp / csp-identifier

2.3.3 Unknown

This states that the CSP referred to is unknown to an agent.

Proposition	csp-unknown
Ontology	FIPA-CCL
Description	This proposition is true iff the referred CSP is unknown to the agent making the statement.
Domain	csp-identifier

2.3.4 Is a Constraint Satisfaction Problem

This proposition can be used to wrap CSPs in a proposition construct for general information passing. The semantic meaning of the message containing such a proposition may be derived from the conversation context.

Proposition	is-csp
Ontology	FIPA-CCL
Description	This proposition is true iff the object referred to is a well formed CSP object.
Domain	csp / csp-identifier

2.3.5 Is an Action Result

The csp-action value is not mandatory since in some cases it may be unnecessary to repeat the specification of the action that led to the result since the action is being referred to may be clear form the context.

Proposition	is-action-result
Ontology	FIPA-CCL
Description	This proposition is true iff the object referred to is the result of an action which is either given in the optional csp-action value or is well defined in the context of the agent conversation.
Domain	ccl-object / ccl-proposition, csp-action

2.4 Ontology Requirements

To ensure that domain ontologies can be easily bound into the content language, FIPA CCL imposes some minimal restrictions on the form of an ontology that is used with it. In particular the ontologies must define items of the following types:

· Types of variables should correspond to the object defined in Section 2.1.16, Domain Variable Type. Variable types define the form of information which variables of that type can express, for example, times, dates, places, airlines, etc.

· Roles of variables should correspond to the object defined in Section 2.1.14, Domain Role Term. A variable role corresponds to the variable’s function in the current problem solving context, for example, 'flight', 'outbound', 'meeting location', etc. Agents can attach roles to variables to keep track of the semantic interpretation of the choice problem.

· Values are the available options for choices and correspond to the domain-term terminals defined in Section 2.1.15. This can be any usefully defined term in the domain ontology.

· Variable domain ranges should correspond the allowed range expressions in the domain, where a range is a well defined set or continuum of domain terms. Domain ranges correspond to the object defined Section 2.1.13, Domain Range. Since some variable domains are often best compactly expressed as ranges rather than enumerated, an ontology may define the legal types of ranges available. Examples include, ranges of time (“working-day” = 8.00am – 5.00pm), ranges of sizes (shoe size = 3 – 12), etc. For some ontologies, domain ranges may be parameterised expressions, for example, a time ontology may include a expression for a range such as hours (start, end) indicating the range of hours between the start and end hours given.

Effectively these restrictions impose typing requirements on the domain ontology to be used with FIPA CCL. How the types are expressed in any particular ontology is application and ontology dependent and hence not addressed in this specification.

3 References

[Dechter92] Constraint Networks, Dechter, R. In: Encyclopedia of Artificial Intelligence, Wiley, pages 276-285, 1992.

[FIPA00061] FIPA ACL Message Structure Specification. Foundation for Intelligent Physical Agents, 2000. http://www.fipa.org/specs/fipa00061/

[Freuder82] A Sufficient Condition of Backtrack-Free Search, Freuder, EC. In: Journal of the ACM, 29(1), pages 24-32, January 1982.

[Mackworth77] Consistency in Networks of Constraints, Mackworth, A. In: Artificial Intelligence, Vol. 8, 1977.

[SamHaroud96] Consistency Techniques for Continuous Constraints, Sam-Haroud, D and Faltings, B. In: Constraints, 1(1), pages 85-118, 1996.

[Tsang94] Foundations of Constraint Satisfaction, Tsang, E. Academic Press, 1994.

[vanBeek97] Constraint Tightness and Looseness Versus Local and Global Consistency, van Beek, P and Dechter, R. In: Journal of the ACM, 44(4), pages 549-566, July 1997.

[Waltz 75] Generating Semantic Descriptions from Drawings of Scenes with Shadows, Waltz, D I. In: The Psychology of Computer Vision, McGraw-Hill, 1975.

4 Normative Annex A — FIPA-CCL XML Based Concrete Syntax

This annex gives a concrete syntax for the FIPA CCL language as an XML DTD. This syntax is the default syntax for FIPA CCL and the only one currently defined. Any agent sending an ACL message with the :content parameter set to FIPA-CCL is assumed to have used this syntax.

4.1 XML DTD

<?xml version="1.0" encoding="UTF-8"?>

<!--=== DTD of the Choice Content Language (CLL). This definition is based in the document "A FIPA Content Language for Expressing Agent Choice: Constraint Choice Language (FIPA-CCL)" ===-->

<!ELEMENT Expression (Object

| Action

| Proposition)>

<!--Definition of an Object in FIPA-CCL-->

<!ENTITY % objects "CSP

| CSP-solution

| CSP-solution-list">

<!ELEMENT Object (CSP

| CSP-solution

| CSP-solution-list)>

<!ATTLIST Object Name ( %objects; ) #REQUIRED>

<!--== CSP ===-->

<!ELEMENT CSP (CSP-variable*, CSP-relation*, CSP-exclusion*)>

<!ATTLIST CSP CSP-ref ID #IMPLIED>

<!--=== CSP-solution ===-->

<!ELEMENT CSP-solution (CSP-variable-assignment*)>

<!ATTLIST CSP-solution href CDATA #REQUIRED>

<!--=== CSP-solution-list ===-->

<!ELEMENT CSP-solution-list (CSP-solution+)>

<!ATTLIST CSP-solution-list href CDATA #REQUIRED>

<!--Definition of an Action in FIPA-CCL-->

<!ENTITY % actions "CSP-give-constraints

| CSP-give-values

| CSP-solve

| CSP-solve-list">

<!ELEMENT Action (CSP-give-constraints

| CSP-give-values

| CSP-solve

| CSP-solve-list)>

<!ATTLIST Action Name (%actions;) #REQUIRED>

<!--=== CSP-give-constraints ===-->

<!ELEMENT CSP-give-constraints (CSP

| CSP-identifier)>

<!--=== CSP-give-values ===-->

<!ELEMENT CSP-give-values (CSP

| CSP-identifier)>

<!--=== CSP-solve ===-->

<!ELEMENT CSP-solve (CSP | CSP-identifier)>

<!--ENTITY % result-values "CSP-solution

| CSP-insoluble

| CSP-solution-list"-->

<!--=== CSP-solve-list ===-->

<!ELEMENT CSP-solve-list (CSP

| CSP-identifier)>

<!--Definition of a Proposition in FIPA-CCL-->

<!ENTITY % propositions "CSP-insoluble

| CSP-soluble

| CSP-unknown">

<!ELEMENT Proposition (CSP-insoluble

| CSP-soluble

| CSP-unknown)>

<!ATTLIST Proposition Name ( %propositions; ) #REQUIRED>

<!--=== CSP-insoluble ===-->

<!ELEMENT CSP-insoluble (CSP

| CSP-identifier)>

<!--=== CSP-soluble ===-->

<!ELEMENT CSP-soluble (CSP

| CSP-identifier)>

<!--=== CSP-unknown ===-->

<!ELEMENT CSP-unknown EMPTY>

<!ATTLIST CSP-unknown href CDATA #REQUIRED>

<!--=== IS-csp ===-->

<!ELEMENT IS-csp (CSP

| CSP-identifier)>

<!--=== IS-action-result ===-->

<!ELEMENT IS-action-result (Action-performed?, Result-obtained)>

<!ELEMENT Result-obtained (Object

| Proposition)>

<!ELEMENT Action-performed (Action)>

<!--Apart from the three main types of items listed above (Actions, Objects and Propositions) there are also other constructs in the CL which form part of the main objects but cannot form valid sentences by themselves.-->

<!--=== CSP-identifier ===-->

<!ELEMENT CSP-Identifier EMPTY>

<!ATTLIST CSP-Identifier href CDATA #REQUIRED>

<!--=== CSP-domain ===-->

<!ELEMENT CSP-domain (Tags*)>

<!ATTLIST CSP-domain Range CDATA #REQUIRED>

<!ELEMENT Tags EMPTY>

<!ATTLIST Tags Name CDATA #REQUIRED>

<!--=== CSP-value ===-->

<!ELEMENT CSP-value (Elements+, Tags*)>

<!ATTLIST CSP-value Npart CDATA #REQUIRED>

<!ELEMENT Elements EMPTY>

<!ATTLIST Elements Value CDATA #REQUIRED>

<!--=== CSP-variable ===-->

<!ELEMENT CSP-variable (Role*, Domain*)>

<!ATTLIST CSP-variable Name CDATA #REQUIRED

Type CDATA #REQUIRED>

<!ELEMENT Role (#PCDATA)>

<!ELEMENT Domain (CSP-range

| CSP-value+

| CSP-value-list)>

<!--=== CSP-range ===-->

<!ELEMENT CSP-range (Tuple-range) >

<!ATTLIST CSP-range Range CDATA #REQUIRED>

<!ELEMENT Tuple-range EMPTY>

<!ATTLIST Tuple-range Values CDATA #REQUIRED>

<!--=== CSP-variable-assignment ===-->

<!ELEMENT CSP-variable-assignment (CSP-value)>

<!ATTLIST CSP-variable-assignment Name CDATA #REQUIRED>

<!--=== CSP-value-list===-->

<!ELEMENT CSP-value-list (List-values, Tags*) >

<!ATTLIST CSP-value-list Npart CDATA #REQUIRED>

<!ELEMENT List-values EMPTY>

<!ATTLIST List-values Values CDATA #REQUIRED>

<!--Constraint Related Items-->

<!--=== CSP-exclusion ===-->

<!ELEMENT CSP-exclusion (Excluded-Values+, Tags*)>

<!ATTLIST CSP-exclusion Variable-name CDATA #REQUIRED>

<!ELEMENT Excluded-Values (CSP-value)>

<!--=== CSP-relation ===-->

<!ENTITY % relation "intentional-Equality

| intentional-Inequality

| Intensional-GreatherThan

| Intensional-LessThan

| Intensional-GreatherThanEqual

| Intensional-LessThanEqual

| Intensional-Empty">

<!ELEMENT CSP-relation (Tags*)>

<!ATTLIST CSP-relation Variables CDATA #REQUIRED

Relation-type (%relation;) #REQUIRED

Indices CDATA #REQUIRED>

5 Informative Annex B — Language Usage

FIPA CCL is primarily intended for information gathering and problem solving for tasks involving multiple interrelated choices. In general information gathering and problem solving tasks can be broken down into four steps[2]:

1. Problem modelling,

2. Information gathering,

3. Information fusion, and,

4. Problem solution.

This section gives a brief overview of using FIPA CCL in each of these steps.

5.1 Step 1: Problem Modelling

Modelling a choice problem in the FIPA CCL language requires the problem to be formulated as a CSP:

· Identifying what the choices are which become the variables in the problem formulation,

· Identifying which options are available for each of the choice which generates the domains of values for each of the variables, and,

· Specifying how choices are related which generates the constraints (relations and exclusions) which apply to problem solutions.

This process is exactly what would be required when formulating problems so that they can be expressed in FIPA CCL messages. The process is in general intuitive, although there may also exist multiple formulations of a particular problem all of which are equivalent in the solution space they describe (although they may be easier or harder to solve depending upon the solution techniques applied).

5.1.1 FIPA Constraint Choice Language Constraint Representations

FIPA CCL uses a particular style of representation for constraints which allows only two types of constraints:

· Exclusions which act on a single variable and are specified as a no-good list, that is, a list of values which this variable may not take.

· Binary intensional relations which act on two variables and are restricted to a closed set of eight general types of relations, that is, the set {=, ¹, <, >, £, ³, ^, null}.

The use of tuple-valued variables allows the language to handle arbitrary n-ary constraints by introducing variables whose values represent the tuples allowed by the constraint and then linking the n variables involved in the n-ary constraints to the tuple valued variable using binary relations. The advantage of this implementation is that solving or consistency engines can be restricted to unary and binary constraints.

As an example of representing n-ary constraints in terms of binary constraints consider a ternary constraint over three variables (Hotel, City and Room-Type):

· Variable: Hotel, Values: {Marriott, Intercontinental, Hyatt-Regency}.

· Variable: City, Values: {New York, Washington, Chicago}.

· Variable: Room-Type, Values: {standard, suite}.

· Constraint: Good-list: {( Hotel: Marriott, City: New York, Room-Type: suite), (Hotel: Intercontinental, City: Washington, Room-Type: standard)}.

This can be converted into the following binary CSP by adding a tuple valued variable which represents the good-list:

· Variable: Hotel, Values: {Marriott, Intercontinental, Hyatt-Regency}.

· Variable: City, Values: {New York, Washington, Chicago}.

· Variable: Room-Type, Values: {standard, suite}.

· Variable: Constraint-1, Values: {(Marriott, New-York, suite), (Intercontinental, Washington, standard)}.

· Constraint: (Intensional-Equality, Variable 1: Hotel, Variable 2: Constraint-1, Indices: {(1, 1)}).

· Constraint: (Intensional-Equality, Variable 1: City, Variable 2: Constraint-1, Indices: {(1, 2)}).

· Constraint: (Intensional-Equality, Variable 1: Room-Type, Variable 2: Constraint-1, Indices: {(1, 3)}).

The same mechanism of using a tuple-valued variable can be used to express constraints which might normally be expressed using an extensional constraint, such as a good list or no-good list, that is, lists of allowed or excluded combinations.

Giving a list of all the allowed combinations of values between a set of variables defines an extensional relation, such as for clothing for example:

· Variable: Hat, Values: {green, red, brown, black}.

· Variable: Shirt, Values: {white, red, pink}.

· Constraint: Good-list: {(Hat: green, Shirt: white), (Hat: red, Shirt: white), (Hat: black, Shirt: red)}.

This relates the two variables Hat and Shirt by giving a list of the allowed combinations. The same type of representation could be used to express combinations which are not allowed and resulting in a no-good list. In FIPA CCL this would be expressed using three variables, using only intensional relations:

· Variable: Hat, Values: {green, red, brown, black}.

· Variable: Shirt, Values: {white, red, pink}.

· Variable: Constraint-Hat-Shirt, Values: {(green, white), (red, white), (black, red)}.

· Constraint: Constraint-Hat: (Intensional-Equality, Variable 1: Hat, Variable 2: Constraint-Hat-Shirt, Indices: {(1, 1)}).

· Constraint: Constraint-Shirt: (Intensional-Equality, Variable 1: Shirt, Variable 2: Constraint-Hat-Shirt, Indices: {(1, 2)}).

The two intensional constraints therefore link the Hat and Shirt variables to a new third variable which contains the list of allowed tuples. This removes any need for lists of valid combinations to be represented as constraints.

5.2 Step 2: Information Gathering

Once a choice problem had been modelled as a CSP, problem information can be added to the CSP representation to constrain or expand the range of options available. This information can be obtained from other agents by sending requests for csp-give-constraints and csp-give-values:

· Requesting csp-give-constraints results in a CSP with more constraints (exclusions or relations) posted on the set of possible combinations, and,

· Requesting csp-give-values results in a CSP with more possible options being added to the CSP variables (choices).

The results of both these actions is a new CSP which can be composed with the original CSP to create a new CSP with more information about the problem being solved. An agent may request information from several sources by:

· Sending the complete CSP to several agents and asking for constraints or values. This case would be most useful if the agents being queried have similar roles in the scenario – e.g. they are all airline flight databases but for different companies. The agent trying to solve the choice problem would receive several sets of information for the same problem.

· Dividing up the whole problem into smaller pieces (each containing a – not necessarily disjoint - subset of variables and constraints) and sending requests about each piece to different information agents. This would be most useful when communicating with agents which have different specialties, that is, one hotel database agent, one airline agent and one ticket booking agent. In each communication the interaction concerns only the part of the problem related to the queried agent’s specialty.

Once information has been gathered the agent solving the problem can pass on to the information fusion step.

5.2.1 Using Tags to Separate Information from Different Sources

FIPA CCL includes a way of tagging values and constraints uniquely which allows problems to include a representation of where information came from. In the results of both the csp-give-constraints and csp-give-values functions the domain values and constraints returned can be grouped together using a tag (a unique symbol). The tags are given in the tags parameter of the csp-value, csp-exclusion and csp-relation items.

5.3 Step 3: Information Fusion

There are two ways of combining CSPs which contain identical sets of variables:

· So that the resulting solution space is the intersection of the solutions of each of the participant CSPs. Hence all solutions to the new CSP satisfy all the participant CSPs. In this document this is referred to as a conjunctive combination.

· So that the resulting solution space is the union of the solutions of each participant CSPs. Here each solution to the new CSP satisfies at least one of the participant CSPs. In this document this is referred to as a disjunctive combination.

These are the basic operations required for compositions. Both operations can be carried out by straightforward algorithms as long as CSPs have the same variables, but may be require transformations to the participant CSPs beforehand.

5.3.1 Using Tags for Information Fusion

The mechanism for combining relations relies on the use of tags to achieve the correct semantics. This is best understood by considering an example. In Figure 1, variables X1 and X2 are linked with an equality constraint and tag T1, the solution space is therefore ((a, a), (b, b)).

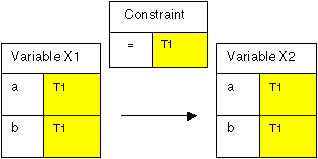
Figure 1: Constraint Problem 1

In Figure 2, the same variables are connected by a ³ constraint[3], but with a different tag T2. Its solution space is ((b, b), (c, b), (c, c)).

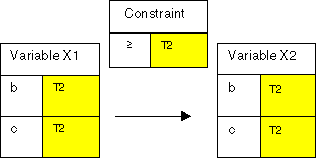
Figure 2: Constraint Problem 2

Hence the tags define two sets of information for the two variables X1 and X2. The information associated with Tag T1 gives on set of possibilities for the variable domains and a constraint. The information associated with Tag T2 gives a second set of domains and a different constraint. Some information (such as the value b in both domains) is common to both information sets.

Exclusions are handled in the same manner simply by treating them as constraints on a single variable. It should also be noted that when relations have the same tags, they can be combined directly by combining their types, that is, £ and ³ combined give =.

5.3.1.1 Conjunctive Combination

Given the two example CSPs in the previous section we can now consider forming the intersection of the two solution spaces described by tags T1 and T2. This intersection would give only the solution ((b, b)) as valid. To do this, we need to intersect the domains for each variable. We then make sure that both constraints apply to the remaining values simultaneously by letting the tags of the remaining values be the union of the tags they had in the original problems, thus making all their constraints applicable (see Figure 3).

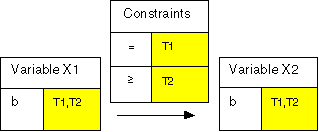
Figure 3: Constraint Problem 3

5.3.1.2 Disjunctive Combination

For the same example we can also form the union of the two solution spaces: a new CSP that has the solution space ((a, a), (b, b), (c, b), (c, c)). To do this, we need take the union of the domains for each variable. We also take the union of the constraints but constraints only apply to the values which have the appropriate tags that is, constraints only apply to the values they applied to in the original problems (see Figure 4).

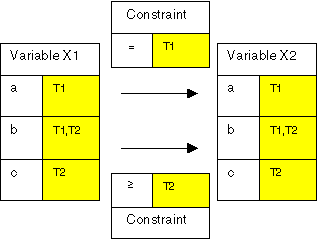
Figure 4: Constraint Problem 4

5.3.2 Information Fusion for Constraint Satisfaction Problems with Non-identical Variable Sets

If two CSPs to be composed do not have exactly the same variables, the two composition operations need to be extended.

5.3.2.1 Conjunctive Composition

This composition is a straightforward extension of the conjunctive composition for the case where variable sets were identical. when composing two CSPs CSP₁ and CSP₂ (to form CSP_Result):

· All constraints from both CSP₁ and CSP₂ hold in CSP_Result (as defined for the standard composition operation),

· All variables from both CSP₁ and CSP₂ are present in CSP_Result, and,

· All variables in CSP_Result must be instantiated s.t. both participant CSPs are satisfied by any solution to the whole CSP_Result.

5.3.2.2 Disjunctive Composition

The disjunctive case is a little more complex. When composing two CSPs CSP₁ and CSP₂ (to form CSP_Result), variables are treated as follows:

· Variables in the intersection CSP₁ CSP₂ (set I): for the variables which exist in both CSPs the required disjunctive composition operation can be directly applied and all variables and constraints between them appear in CSP_Result.

· Variables outside the intersection CSP₁ CSP₂ (set NI): these variables exist in only one of the participant CSPs. All these variables are also added to CSP_Result but are modified in the process by adding a special value “*” to each of their domains, where “*” stands for “unused”.

To add the variables in CSP₁ which do not appear in CSP₁ (I.e. are in the intersection of CSP₁ and NI – call this set NI₁):

1. Generate a new unique tag T₁.

2. For each variable v in NI₁:

1. Add the “*” value (or a tuple of “*” values, depending on its type) into the domain of v like any other value (unless the domain of v already contains such a value).

2. Add the tag T₁ to the “*” value, to the relations which involve v and to all values in the domain of variables that participate in these relations (if v already contained the “*” value – add the tag to the previous “*” value).

3. Add all the variables in IN₁, their related relations and relations between variables in IN₁ and I to CSP_Result.

The same process is performed for the variables in CSP₂ and not in CSP₁ (set IN₂) but with a different tag generated in step 1 of the algorithm.

Finally, all the “*” values are considered compatible with any relation, this makes it possible to distinguish solutions to the problem which assign a value to the variable in question and those that do not. The algorithm uses the tag mechanism to distinguish the new variables and relations from the existing ones: since the “*” value is compatible with any relation, the set of solutions of the revised CSP is exactly the solutions of the original CSP with the “*” value added for the new variable. Furthermore, the unique tag ensures that this same property continues to hold when the new CSP is combined with another one.

5.4 Step 4: Problem Solving

Once a problem has been modelled, information gathered and composed to form a single choice problem, then this can be solved. The semantic meaning behind the variables and constraints in the task model can be stripped away during the solution process and the problem can be solved as a generic CSP. This allows powerful CSP problem solving algorithms to be applied.

In the context of the FIPA CCL language there are two main ways to solve a constructed CSP problem:

· Implementation of one (or several) solution algorithms in the problem solving agent. Solution algorithms range from very simple compact approaches to elaborate specialised techniques. The next section gives an example of a simple search algorithm which would suffice for most small CSP problems. More advanced algorithms can be found in, among others; [Tsang94], the proceedings of major AI conferences and the proceedings of specialist constraints conferences such as Constraint Programming.

· Usage of a dedicated CSP solving agent which implements a suite of algorithms for solving algorithms for generic CSPs. Such solver agents can be requested to solve choice problems using the FIPA CCL language actions csp-solve and csp-solve-list.

5.4.1 Simple Constraint Satisfaction Problem Search Algorithm

This section gives a basic solution algorithm for CSP problems to provide the minimum for problem solving using FIPA CCL. The backtracking search algorithm given here instantiates variables in some fixed order and is perhaps the most commonly used CSP search techniques (many advanced methods are derived from it). The following gives the general idea:

1. Choose some fixed order for the variables in the set of variables V. Choose some fixed order for each of the variable domains D_i. Using these orderings repeat the following:

2. Choose the next uninstantiated variable v_i in the order of V:

1. If all the variables in V have been assigned values then a solution has been found and the procedure terminates.

2. Otherwise proceed to step 2.

3. Assign to v_i the next available value d from its domain D_i:

1. IF D_i is empty (there are no remaining values for v_i) then backtrack – undo the previous variable assignment made (v_i-1), mark v_i-1 as unassigned and continue from step 1.

2. Otherwise continue to step 3.

4. Check that none of the constraints in C which involve variable v_i are violated by assigning d to v_i:

1. IF no such constraint in C is violated, mark v_i as instantiated with value d and proceed to the next variable (go to step 1).

2. IF a constraint is violated the by this assignment then backtrack - keep v_i as uninstantiated, remove the value d from the domain D_i and go back to step 2.

The procedure also terminates if it backtracks to step 2 and the first variable in the sequence has no remaining possible values in its domain. This indicates that all value combinations are invalid and the CSP has no solution.

This procedure is sound and complete since the backtracking procedure essentially explores the search tree of possible variable assignment combinations. Constraints are checked at each step (ensuring a non-valid combination is never allowed) and the backtracking step is eventually forced to explore the whole search tree.

5.5 References

[Dechter92] Constraint Networks, Dechter, R. Encyclopaedia of Artificial Intelligence, Wiley, pages 276-285, 1992.

[Tsang94] Foundations of Constraint Satisfaction, Tsang, E. Academic Press, 1994.

---

[1] The restriction to two variables here (rather than 2 or more) corresponds to the restriction of FIPA-CCL to binary relations only.

[2] [Dechter92] and [Tsang94] provide good introductions to modelling problems as CSPs.

[3] Defined over the alphabetical order with a/A as the largest.